ℐl cifrario che andiamo a vedere è una semplice evoluzione del cifrario
di Cesare che si basa sui concetti di algebra lineare e cioè sul
calcolo matriciale. Ho tratto l'idea da un articolo di Hacker
Journal ma probabilmente queste idee fanno parte dell'introduzione dei
testi universitari che parlano di crittografia. Per una trattazione
matematica completa del cifrario questo
articolo di matematica superiore tratta l'argomento in modo completo.
Qui si affronta il problema con meno strumenti matematici e si incorre nel problema di avere la frase crittografata molto lunga. Questo è dovuto all'assenza della aritmetica modulare. Comunque può essere interessante vedere una prima approssimazione del cifrario matriciale che svilupperemo in questo articolo che segue.
Per cifrare il messaggio che supponiamo in caratteri ascii, lo dividiamo in blocchi di N×N caratteri e lo moltiplichiamo per la matrice A che supponiamo quadrata di ordine N (matrice N×N). Per la decifratura è sufficiente moltiplicare il messaggio cifrato diviso in blocchi di N×N caratteri, per la chiave A-1.
Un teorema ci dice che A è invertibile sse (se e solo se) ha determinante non nullo, un altro teorema ci dice che deve avere determinante pari a ±1 sse vogliamo che A-1 abbia valori interi (cioè matrice a elementi in \( \mathbb{Z} \)), cosa molto comoda.
Quest'ultimo teorema deriva dal teorema di Binet che afferma:
\[ \large |A| \cdot |A^{-1}| = 1 \] Con OCTAVE possiamo fare tutti i calcoli del caso, riporto immediatamente di seguito i comandi direttamente inseribili in Octave per seguire l'esempio. Se scegliamo:
\[ \large \begin{bmatrix} 1 & 2 \\ 3 & 5 \end{bmatrix} \] A=[1,2;3,5]
il determinante è:
\[ \large |A| = 1 \cdot 5 - 2 \cdot 3 = -1 \] det(A)
l'inversa ha quindi valori in \( \mathbb{Z} \):
\[ \large \begin{bmatrix} -5 & 2 \\ 3 & -1 \end{bmatrix} \] inv(A)
supponiamo che il messaggio sia:
M=[1,2,3,4,5,6,7,8,9]
dove per facilità di comprensione del problema possiamo fare corrispondere al numero 1 la lettera a, al numero 2 la lettera b, ecc, quindi M sarà anche:
M=[a,b,c,d,e,f,g,h,i,l]
dividiamolo in vettori di dimensione 2:
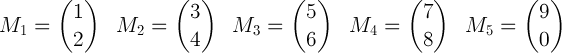
m1=[1;2]
m2=[3;4]
m3=[5;6]
m4=[7;8]
m5=[9;0]
il messaggio cifrato C sarà:
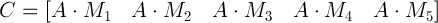
C=[A*m1;A*m2;A*m3;A*m4;A*m5]
che avrà questo codice numerico:
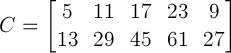
ovvero mettendolo in una unica riga:
C = [5 13 11 29 17 45 23 61 9 27]
Come si vede, senza l'aritmetica modulare si incorre in "testo" cifrato che è più "complesso" del testo di partenza.
L'operazione di decifratura è del tutto simmetrica, si scompone il messaggio cifrato C in 5 sotto-messaggi:
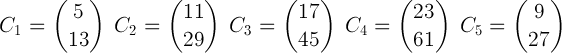
c1=[05;13]
c2=[11;29]
c3=[17;45]
c4=[23;61]
c5=[09;27]
e si riottiene il messaggio:
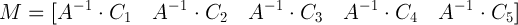
a=inv(A)
M=[a*c1;a*c2;a*c3;a*c4;a*c5]
e cioè:
M=[1,2,3,4,5,6,7,8,9]
M=[a,b,c,d,e,f,g,h,i,l]
Esistono dei piccoli problemi pratici come ad esempio il caso di messaggi a lunghezza non multipla dell'ordine della matrice scelta, come nel caso mostrato e poi il problema di riportare in codifica ASCII il messaggio cifrato.
Il primo si può risolvere riportando a inizio messaggio la lunghezza del messaggio stesso e aggiungendo nei posti liberi in coda dei caratteri casuali, il secondo si può risolvere esprimendo in base 127 (o quanti sono i caratteri ASCII stampabili) il messaggio oppure utilizzando una compressione che dia una uscita ASCII.
Per quanto riguarda la determinazione di una matrice N×N che abbia determinante unitario si ricade nella teoria delle matrici di SL(N,Z). Se qualcuno è interessato mi posso informare riguardo questa teoria che però a prima vista pare complessa e inoltre non ho trovato funzioni di Octave che le generino. Mi pare di avere capito che vengano anche chiamate matrici monodrome.
Kensan.it
Se il problema fosse difficile si può ricorrere alla matematica delle frazioni visto che l'inversa di una matrice a elementi interi è una matrice a elementi frazionari.
Nota: Il cifrario di Cesare ottiene il testo cifrato aumentando di tre il codice ASCII di ogni lettera del messaggio in chiaro, per esempio "cesare" diventa "fhvduh". Corrisponde in pratica a un ROT-3.
Prendiamo una matrice quadrata di dimensione 4 e triangolare con tutti i suoi elementi in \( \mathbb{Z} \):

essendo una matrice di Gauss il determinante è pari al prodotto degli elementi della diagonale quindi ovviamente:

Essendo la matrice inversa a meno del segno composta da elementi che sono tutti l'inverso del determinante di A moltiplicato per il determinate di un minore si ha che se tutti i minori hanno determinante in \( \mathbb{Z} \) allora anche A-1 ha tutti i suoi elementi in \( \mathbb{Z} \). Inoltre il determinante di una matrice con elementi in \( \mathbb{Z} \) è sempre un numero intero, data la ricorsività dello sviluppo di Laplace che coinvolge solo somme e prodotti tra gli elementi di una matrice. Quindi tutti i minori di A hanno determinante intero e di conseguenza A-1 ha tutti i suoi elementi in \( \mathbb{Z} \).
La matrice inversa è la seguente:

L'inversa è ancora triangolare e questa è una regola generale.
Per avere ottenuto questo risultato le imposizioni che abbiamo fissato sulla matrice A sono solo:
quindi il resto degli elementi della matrice possono essere fissati in modo casuale per ottenere un cifrario matriciale casuale.
Inoltre si possono effettuare su A le mosse di Gauss che non cambiano il determinante di A (a meno del segno) e che quindi lasciano A-1 con elementi interi.
1) scambiare tra loro due righe;
2) moltiplicare una riga per uno scalare n non nullo;
3) sostituire una riga della matrice con quella che si ottiene sommando a essa un multiplo di un'altra riga.
escludendo la 2) in quanto comporta che il det(A) diventa det(A) · n, le opzioni 1) e 3) non cambiano il determinante che rimarrà unitario a meno del segno. Le due opzioni valgono pure per le colonne.
Per esempio possiamo sommare la prima colonna a tutte le altre colonne:
A = [C1 C2 C3 C4] => B = [C1 (C2+C1) (C3+C1) (C4+C1)]

Inoltre possiamo sommare l'ultima riga a tutte le altre:
B = [R1' R2' R3' R4'] ' => C = [(R1'+R4') (R2'+R4') (R3'+R4') R4']'

Ancora otteniamo:


Tale matrice C-1 e la matrice C proviamo ad usarle per crittografare la parola "segreto":
"segreto" => v = [115, 101, 103, 114, 101, 116, 111, 0] = [v1, v2]
C·v1 = [1819 | 2353 | 2990 | 1386]
C·v2 = [1443 | 1887 | 2442 | 1115]
e applicando la matrice inversa C-1 otteniamo il codice ascii di "segreto", come si può vedere con il programma di matematica on line WolframAlpha.
Essendo la matrice C con tutti i suoi elementi non negativi, i numeri di uscita dal prodotto tra il messaggio e la matrice sono elevati, per cui si può ridurre C·v considerando che (se si usano solo lettere minuscole) il codice ascii di "a" è 97 per cui sottraendo da v il codice ascii di "a" si ha:
"segreto" => v = [18, 4, 6, 17, 4, 19, 14, 0] = [v1, v2]
e il codice cifrato diventa:
C·v1 = [170 | 219 | 274 | 125] = 170+219*701+274*701^2+125*701^3 = 43193810188
C·v2 = [182 | 238 | 308 | 145] = 182+238*701+308*701^2+145*701^3 = 50099973173
numeri che si posso convertire in ascii mediante questo convertitore che usa le prime 10 cifre numeriche (0..9) e poi le lettere maiuscole dal A..Q per rappresentare i numeri in base 25:
C·v = [71N13L7D 8555N71N]
Quindi:
"segreto" => "71N13L7D8555N71N"
Qui si affronta il problema con meno strumenti matematici e si incorre nel problema di avere la frase crittografata molto lunga. Questo è dovuto all'assenza della aritmetica modulare. Comunque può essere interessante vedere una prima approssimazione del cifrario matriciale che svilupperemo in questo articolo che segue.
Per cifrare il messaggio che supponiamo in caratteri ascii, lo dividiamo in blocchi di N×N caratteri e lo moltiplichiamo per la matrice A che supponiamo quadrata di ordine N (matrice N×N). Per la decifratura è sufficiente moltiplicare il messaggio cifrato diviso in blocchi di N×N caratteri, per la chiave A-1.
Un teorema ci dice che A è invertibile sse (se e solo se) ha determinante non nullo, un altro teorema ci dice che deve avere determinante pari a ±1 sse vogliamo che A-1 abbia valori interi (cioè matrice a elementi in \( \mathbb{Z} \)), cosa molto comoda.
Quest'ultimo teorema deriva dal teorema di Binet che afferma:
\[ \large |A| \cdot |A^{-1}| = 1 \] Con OCTAVE possiamo fare tutti i calcoli del caso, riporto immediatamente di seguito i comandi direttamente inseribili in Octave per seguire l'esempio. Se scegliamo:
\[ \large \begin{bmatrix} 1 & 2 \\ 3 & 5 \end{bmatrix} \] A=[1,2;3,5]
il determinante è:
\[ \large |A| = 1 \cdot 5 - 2 \cdot 3 = -1 \] det(A)
l'inversa ha quindi valori in \( \mathbb{Z} \):
\[ \large \begin{bmatrix} -5 & 2 \\ 3 & -1 \end{bmatrix} \] inv(A)
supponiamo che il messaggio sia:
M=[1,2,3,4,5,6,7,8,9]
dove per facilità di comprensione del problema possiamo fare corrispondere al numero 1 la lettera a, al numero 2 la lettera b, ecc, quindi M sarà anche:
M=[a,b,c,d,e,f,g,h,i,l]
dividiamolo in vettori di dimensione 2:
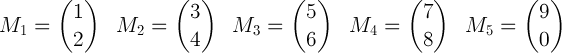
m1=[1;2]
m2=[3;4]
m3=[5;6]
m4=[7;8]
m5=[9;0]
il messaggio cifrato C sarà:
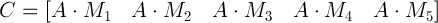
C=[A*m1;A*m2;A*m3;A*m4;A*m5]
che avrà questo codice numerico:
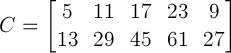
ovvero mettendolo in una unica riga:
C = [5 13 11 29 17 45 23 61 9 27]
Come si vede, senza l'aritmetica modulare si incorre in "testo" cifrato che è più "complesso" del testo di partenza.
L'operazione di decifratura è del tutto simmetrica, si scompone il messaggio cifrato C in 5 sotto-messaggi:
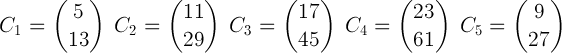
c1=[05;13]
c2=[11;29]
c3=[17;45]
c4=[23;61]
c5=[09;27]
e si riottiene il messaggio:
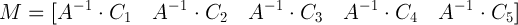
a=inv(A)
M=[a*c1;a*c2;a*c3;a*c4;a*c5]
e cioè:
M=[1,2,3,4,5,6,7,8,9]
M=[a,b,c,d,e,f,g,h,i,l]
Esistono dei piccoli problemi pratici come ad esempio il caso di messaggi a lunghezza non multipla dell'ordine della matrice scelta, come nel caso mostrato e poi il problema di riportare in codifica ASCII il messaggio cifrato.
Il primo si può risolvere riportando a inizio messaggio la lunghezza del messaggio stesso e aggiungendo nei posti liberi in coda dei caratteri casuali, il secondo si può risolvere esprimendo in base 127 (o quanti sono i caratteri ASCII stampabili) il messaggio oppure utilizzando una compressione che dia una uscita ASCII.
Per quanto riguarda la determinazione di una matrice N×N che abbia determinante unitario si ricade nella teoria delle matrici di SL(N,Z). Se qualcuno è interessato mi posso informare riguardo questa teoria che però a prima vista pare complessa e inoltre non ho trovato funzioni di Octave che le generino. Mi pare di avere capito che vengano anche chiamate matrici monodrome.
Kensan.it
Se il problema fosse difficile si può ricorrere alla matematica delle frazioni visto che l'inversa di una matrice a elementi interi è una matrice a elementi frazionari.
Nota: Il cifrario di Cesare ottiene il testo cifrato aumentando di tre il codice ASCII di ogni lettera del messaggio in chiaro, per esempio "cesare" diventa "fhvduh". Corrisponde in pratica a un ROT-3.
Approfondimento
Prendiamo una matrice quadrata di dimensione 4 e triangolare con tutti i suoi elementi in \( \mathbb{Z} \):
essendo una matrice di Gauss il determinante è pari al prodotto degli elementi della diagonale quindi ovviamente:
Essendo la matrice inversa a meno del segno composta da elementi che sono tutti l'inverso del determinante di A moltiplicato per il determinate di un minore si ha che se tutti i minori hanno determinante in \( \mathbb{Z} \) allora anche A-1 ha tutti i suoi elementi in \( \mathbb{Z} \). Inoltre il determinante di una matrice con elementi in \( \mathbb{Z} \) è sempre un numero intero, data la ricorsività dello sviluppo di Laplace che coinvolge solo somme e prodotti tra gli elementi di una matrice. Quindi tutti i minori di A hanno determinante intero e di conseguenza A-1 ha tutti i suoi elementi in \( \mathbb{Z} \).
La matrice inversa è la seguente:
L'inversa è ancora triangolare e questa è una regola generale.
Per avere ottenuto questo risultato le imposizioni che abbiamo fissato sulla matrice A sono solo:
- diagonale di A contenente solo 1
- elementi di A tutti interi (in \( \mathbb{Z} \))
- A triangolare
quindi il resto degli elementi della matrice possono essere fissati in modo casuale per ottenere un cifrario matriciale casuale.
Inoltre si possono effettuare su A le mosse di Gauss che non cambiano il determinante di A (a meno del segno) e che quindi lasciano A-1 con elementi interi.
1) scambiare tra loro due righe;
2) moltiplicare una riga per uno scalare n non nullo;
3) sostituire una riga della matrice con quella che si ottiene sommando a essa un multiplo di un'altra riga.
escludendo la 2) in quanto comporta che il det(A) diventa det(A) · n, le opzioni 1) e 3) non cambiano il determinante che rimarrà unitario a meno del segno. Le due opzioni valgono pure per le colonne.
Per esempio possiamo sommare la prima colonna a tutte le altre colonne:
A = [C1 C2 C3 C4] => B = [C1 (C2+C1) (C3+C1) (C4+C1)]
Inoltre possiamo sommare l'ultima riga a tutte le altre:
B = [R1' R2' R3' R4'] ' => C = [(R1'+R4') (R2'+R4') (R3'+R4') R4']'
Ancora otteniamo:
Tale matrice C-1 e la matrice C proviamo ad usarle per crittografare la parola "segreto":
"segreto" => v = [115, 101, 103, 114, 101, 116, 111, 0] = [v1, v2]
C·v1 = [1819 | 2353 | 2990 | 1386]
C·v2 = [1443 | 1887 | 2442 | 1115]
e applicando la matrice inversa C-1 otteniamo il codice ascii di "segreto", come si può vedere con il programma di matematica on line WolframAlpha.
Essendo la matrice C con tutti i suoi elementi non negativi, i numeri di uscita dal prodotto tra il messaggio e la matrice sono elevati, per cui si può ridurre C·v considerando che (se si usano solo lettere minuscole) il codice ascii di "a" è 97 per cui sottraendo da v il codice ascii di "a" si ha:
"segreto" => v = [18, 4, 6, 17, 4, 19, 14, 0] = [v1, v2]
e il codice cifrato diventa:
C·v1 = [170 | 219 | 274 | 125] = 170+219*701+274*701^2+125*701^3 = 43193810188
C·v2 = [182 | 238 | 308 | 145] = 182+238*701+308*701^2+145*701^3 = 50099973173
numeri che si posso convertire in ascii mediante questo convertitore che usa le prime 10 cifre numeriche (0..9) e poi le lettere maiuscole dal A..Q per rappresentare i numeri in base 25:
C·v = [71N13L7D 8555N71N]
Quindi:
"segreto" => "71N13L7D8555N71N"












