ℒa sicurezza di una password dipende da quanto è disposto a pagare il
nostro nemico per crakkarla, cioè per venire a conoscenza della sua forma
esplicita. Spesso la password è sotto forma di un hash e spesso si usa lo
sha256 che è un algoritmo di hash. È disponibile l'hash e da questo è molto
difficile risalire alla password in quanto l'hash è un algoritmo non
invertibile.
Vediamo qualche esempio:
"password123"
e abbiamo ottenuto l'hash:
"ef92b778bafe771e89245b89ecbc08a44a4e166c06659911881f383d4473e94f"
Il problema del cracker è invertire l'hash ovvero lui ha a disposizione il numero esadecimale di 64 cifre qui sopra e deve trovare a che password corrisponde. L'unico modo di risolvere il problema è provare tutte le combinazioni di password, calcolare l'hash e poi vedere se l'hash calcolato corrisponde a quello che ha in mano. Se corrisponde allora ha trovato la parola segreta.
Poiché provare tutte le combinazioni è molto lungo si cercano delle scorciatoie e cioè si usa il fatto che le persone non sono dei computer e che tengono in mente solo parole segrete fatte in un certo modo. Per esempio la gente si ricorda una parola contenuta nei dizionari seguita da un numero oppure si ricorda uno schema di lettere che c'è nella tastiera, per esempio qwerty oppure qazwsxedc. La prima password, qwerty, non è altro che la prima riga delle lettere sulla tastiera, la seconda parola segreta, qazwsxedc, non è altro che le prime tre colonne delle lettere sulla tastiera.
I dizionari delle principali lingue contengono pochi termini, ogni uno circa 20 mila termini, quindi provando 100 mila password già si possono crakkare le parole segrete più facili. Infatti se supponiamo di prendere in considerazione 5 lingue, si ha che una password di una sola parola in una qualsiasi di queste 5 lingue è crakkabile in 5*20'000 tentativi. Aggiungendo alla fine della parola del dizionario tutti i numeri compresi tra 0 e 9999, si rende la ricerca un po' più difficile. In quest'ultimo caso i tentativi da fare ovvero gli hash da calcolare sono un po' di più ovvero 1 miliardo.
Nel caso si usi la forma della tastiera per inventarsi la parola segreta allora i tentativi da fare per il cracker non sono molti, probabilmente sotto i 10 mila considerando tutti i possibili schemi e anche con un numero finale di 4 cifre si sta sotto il miliardo.
Per il cracker il problema è quindi risolvibile con 2 miliardi di prove sia se usiamo una parola del dizionario sia se usiamo lo schema della tastiera. La domanda a questo punto è: ma quanto tempo impiega un computer per fare 2 miliardi di hash con l'algoritmo sha256? La risposta è: poco tempo.
Ci sono macchine che calcolano l'hash a miliardi in un secondo e comprando decine o migliaia di queste macchine (lo può fare lo Stato americano oppure la mafia o altre organizzazioni) si possono calcolare anche mille o più miliardi di hash al secondo. Quindi in un secondo la password che abbiamo visto sopra è scovabile.
Veniamo alla seconda domanda. C'è un limite a queste macchine che calcolano così tanti hash al secondo? La risposta è affermativa. Queste macchine che adesso si chiamano ASIC ma che in futuro si evolveranno in macchine più potenti, hanno un grosso limite ovvero consumano energia elettrica, ogni hash costa una certa energia spesa.
In Italia l'energia elettrica ha un prezzo all'utente finale di 20 centesimi di euro al chilowattora, a livello industriale costa meno della metà, quindi uno Stato può pagarla un po' meno ma ha comunque un costo ingente. All'estero la corrente si paga di meno ma comunque mai sotto il costo industriale di 6 centesimi di dollaro al chilowattora. L'energia costa dovunque.
Le migliori macchine di adesso, le ASIC, per calcolare mille miliardi di hash (1 Terahash) consumano 0.4 milionesimi di euro in corrente elettrica. Con gli ASIC la nostra password, quella vista sopra, ha un costo in termini energetici irrisorio, quindi non è una parola segreta "sicura".
Veniamo alla domanda che mi ha ispirato per scrivere questo testo:
Facciamo qualche esempio. La password casuale VRnkgxqgTKoK è composta da sole lettere maiuscole e minuscole dell'alfabeto inglese e ha un numero di tentativi che il cracker deve fare per scovarla pari a 390877006486250192896. Considerando il costo di 0.4 milionesimi di euro per 1 miliardo di tentativi (Hash), si ha:
Il costo energetico è di 150 euro.
La password casuale iktpxmwritiw è composta da 12 lettere minuscole su un alfabeto inglese di 25 lettere e ha un numero di hash che il cracker deve calcolare per scovarla pari a 95428956661682176 con un costo elettrico relativo pari a 4 centesimi di euro.
Aggiungendo alla password qui sopra il numero finale casuale 7909 si aumenta il costo energetico e si arriva a 240 euro. La parola segreta complessiva è iktpxmwritiw7909.
In conclusione per proteggere una informazione che vale qualche centinaia di euro una password di 12 lettere minuscole casuali dell'alfabeto inglese seguita da un numero di 4 cifre casuali è sufficiente.
Generiamo tramite un computer o una app di un telefono una password completamente casuale (avendo abbastanza entropia) di 12 lettere prese però dall'alfabeto italiano di 21 caratteri, seguiti da un numero altrettanto casuale di 4 cifre. Valore: 30 euro. Il mio generatore mi ha dato:
zgrvuhstmdtg5218
Per memorizzare una tale parola segreta si può sfruttare una particolarità della mente umana e cioè che è facile memorizzare una storiella. Quindi creiamo una storiella che abbia come prima lettera delle parole le lettere zgrvuhstmdtg5218. Per quanto riguarda il numero va imparato a memoria.
La storiella va scelta con cura, per esempio:
Per quanto riguarda creare la password generata in modo casuale ci sono moltissimi algoritmi che lo fanno: per Firefox ci sono addon che si installano con un click come pwgen.
Man mano che passano gli anni il costo energetico per hash diminuisce e si passa dagli attuali 0.4 milionesimi di euro per terahash a valori minori. È un processo lento in parte contrastato dal fatto che l'energia elettrica costa sempre di più. Tutte le organizzazioni e tutti i cracker sono sottoposti alla legge economica del costo dell'energia, nessuno escluso.
In particolare anche la NSA americana che si vocifera abbia mezzi potentissimi, non può scovare una password che abbia un valore pari all'intera ricchezza americana prodotta in un anno: il PIL USA. Lo stesso vale per la mafia ma entrambi hanno mezzi più efficaci per farci rivelare la parola segreta anche se non vogliamo rivelarla: Guantanamo per quanto riguarda gli americani e la lupara bianca per la mafia.
Per una password che non debba proteggere un grande valore si possono usare dei servizi on line oppure una app scaricata sul proprio cellulare. Un servizio è ad esempio quello di Proton Password-generator che impostato su password di 22 caratteri (alfabeto inglese), minuscolo, senza simboli e numeri da la pwd:
wqzdkdbemcadrvunxauavm
togliendo i caratteri del solo alfabeto inglese (jkwxy) si ha:
qzddbemcadrvunauavm (19 caratteri)
che è utile per fissare la nostra password casuale nella parte delle lettere dell'alfabeto italiano. Per i numeri usiamo il servizio on line per generare casualmente un numero di 4 cifre, ottengo:
2p01yf3hcbrv8t4qhhfp4w
estraggo le sole cifre ed ho:
2013844 (7 cifre)
A questo punto posso costruire la mia password completamente casuale prendendo i primi enne caratteri di «qzddbemcadrvunauavm» e le prime emme cifre di «2013844», ottenendo la password di n+m caratteri.
Nei commenti un lettore mi ha chiesto come si calcolano tutti i tentativi da fare per scoprire una pwd (password). La risposta completa si trova nei libri di matematica ma qui diamo degli spunti.
Supponiamo di avere un alfabeto α di simboli di questo tipo:
α ={a, b, c}
e di avere una parola composta da due soli simboli. Quante parole differenti si possono formare? Il problema si può facilmente risolvere costruendo una matrice bidimensionale ovvero di dimensione 2 pari al numero di simboli della nostra parola (2):
mettendo nella casella prima la lettera corrispondente della riga e poi la lettera della colonna, formiamo per ogni casella una parola di due caratteri. Così abbiamo costruito tutte le combinazioni di una parola di due lettere con un alfabeto di 3 simboli. È facile rispondere quante sono le possibili combinazioni: sono 3×3 ovvero il numero di simboli di α elevato alla potenza 2 perché 2 è la lunghezza della parola: 32.
È facile immaginare che per trovare tutte le combinazioni di una parola di tre simboli del tipo «cab» è necessario passare dalla matrice bidimensionale a quella tridimensionale: un cubo di Rubik per intenderci. Con l'immaginazione pensiamo alla matrice qui sopra con l'aggiunta di tre simboli che escono dallo schermo verso di noi: a, b, c. Si formeranno 3×3×3 caselline cubiche, ogni una delle quali possiamo riempirla con la parola di tre simboli fatta prendendo prima la casella delle righe, poi quella delle colonne e poi quella che esce dallo schermo. L'immagine del cubo che segue può aiutare:
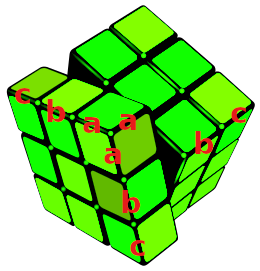
Tutte le possibili combinazione di una parola di tipo «cab» sono quindi 33 come le caselle del cubo qui sopra raffigurato. Analogamente per una parola di lunghezza 4 le combinazioni sono 34. Ecc, ecc. Se α ={a, b, c, d, e, f, g, h, i, l, m, n, o, p, q, r, s, t, u, v, z} una parola del tipo «qaz» ha 213 combinazioni perché corrisponde a un cubo di lato 21. Se la parola è di 12 lettere allora tutte le possibili combinazioni sono:
2112
Gli altri concetti sono una variante di questi concetti appena esposti come giustapporre due password: «zgrvuhstmdtg» + «5218» = «zgrvuhstmdtg5218» da un numero di combinazioni che è il prodotto del numero di combinazioni degli elementi.
Aggiornamento 27 gen 2024: Il sito Hash rate Index riporta dati sempre aggiornati relativi alle macchine per minare bitcoin, quel che ci interessa qui è quanto consumano le migliori macchine ASIC per fare Hash. Nella data di questo aggiornamento siamo arrivati a circa 26 joule per TH (Tera Hash).
Domanda: Quanto costa fare 1 mille miliardi di tentativi ovvero 1 THash?
Partiamo dalle basi e calcoliamo quanto è l'energia di 1 joule in termini di kWh:
1 kWh = 1000W×1h = 1000W×3600s = 3.6×106 j
1 j = 0.278×10-6 kWh
visto il costo dell'elettricità che di solito viene preso a livello industriale pari a:
0.06 €/kWh
si ha che l'energia consumata da queste macchine ASIC per minare 1 TH è pari a:
26 j = 26×0.278×10-6 kWh = 7.22×10-6 kWh
con un costo economico pari a:
Costo di 26 j = 7.22×10-6 kWh × 0.06 €/kWh = 0.433×10-6 €
con questa cifra si realizzano 1 TH ovvero:
1×1012 Hash
quindi il costo per Hash è pari a:
Costo di 1 Hash = Costo di 26 j / 1×1012 = 0.433×10-6 € / 1×1012 = 0.433×10-18 €
Kensan.it 1 € = Costo di 2.31×1018 Hash
All'incirca occorre realizzare una password che abbia un numero di combinazioni pari a 1018 per farla costare 1 € in prezzo dell'energia.
Visto che con 11 lettere minuscole e 4 numeri decimali completamente casuali si raggiunge il numero di combinazioni pari a:
Numero combinazioni password «abcdefghilm1234» = 2111 × 104 = 3.5×1018
si ha che questa lunghezza di password casuale ha un prezzo di 1 €. Occorre quindi aggiungere agli 11 caratteri minuscoli tante lettere quanto grande è il prezzo che vogliamo raggiungere. Ecco una tabellina:
Cui aggiungere il numero da 4 cifre. Quindi già con una password di 16 caratteri e 4 cifre decimali ha un prezzo in energia pari al milione di euro, quindi sufficiente per molti usi.
Aggiornamento 30 mag 2024: Una notizia letta sul giornale on line HWupgrade ha attirato la mia attenzione su un caso di una persona molto attenta alla questione sicurezza informatica e che ha salvato una password di 20 caratteri generata da un generatore di password di nome RoboForm, in un file di testo crittografato con il programma TrueCrypt. Il file testuale crittografato era protetto da una password che la persona in questione non ha dimenticato ma sfortunatamente non ha eseguito alcun backup del file di testo.
Quella lunga parola di 20 caratteri era la porta d'ingresso per accedere a un portafoglio bitcoin (bitcoin wallet). Nel 2013, anno della creazione della parola segreta di 20 caratteri, il bitcoin valeva molto poco e il protagonista dell'articolo ne possedeva 43.6 per un totale di circa 4'000 € di allora. Forse per questo che il back up non era importante ma sfortuna volle che il file di testo crittografato da TrueCrypt andasse corrotto irrimediabilmente e con esso anche il suo contenuto, ovvero la lunga password.
Adesso che ogni bitcoin vale oltre 60 mila euro (63 mila in questo momento), il protagonista ha cercato ogni mezzo per accedere al bitcoin wallet contenente 43.6 BTC peer un valore di milioni di euro. Una coppia di Hacker si è incaricata del salvataggio (dietro compenso) e dato che il file di testo corrotto non esiste più, hanno puntato la loro attenzione sul generatore di password RoboForm, cercando di vedere se ci sono delle falle.
Infatti provare tutte le combinazioni di una parola di 20 caratteri che usi come simboli oltre che le 25 lettere dell'alfabeto inglese, altri 25 del maiuscolo, più i numeri e più i simboli, non è una operazione che si può eseguire prima della fine dell'universo e comunque non in tempi umani.
Hanno però visto che RoboForm non genera password casuali e che impostando la data dell'orologio del PC, le password generate erano limitate a un piccolo insieme. Hanno fatto delle ipotesi sulla data dal 1 marzo all'1 giugno 2013 e sui caratteri, ipotizzando che non contenesse simboli sempre per via di difetti di RoboForm che in alcuni/diversi casi non generava simboli speciali. Questo li ha portati a provare tutte le combinazioni di un numero limitato di password e a trovare la parola chiave di 20 caratteri che ha sbloccato il portafoglio bitcoin contenente 43.6 bitcoin.
Sicuramente la morale di questa storia è quella di fare il backup dei file importanti, soprattutto quando contengono password. Per quanto riguarda l'argomento di questo articolo ovvero la sicurezza di una password, il suggerimento è quello di non usare il tool come RoboForm o quelli da me indicati all'inizio del testo per creare parole segrete di una certa importanza.
Un metodo sicuro per generare lettere e numeri casuali è quella manuale e antico dei dadi, vediamo come.
Per facilitare il compito potete scaricare il foglio elettronico seguente e inserire i lanci ripetuti di un dado a 6 facce nella colonna "C" incorniciata di rosso con 21 lanci. Otterrete la Password numerica e quella testuale automaticamente ma di lunghezza limitata. Scartate i primi due o tre caratteri e le prime due o tre cifre in quanto non sono equiprobabili per via della conversione. Facendo altre serie di 21 lanci potete allungare la vostra password di quanto volete giustapponendo le password ottenute tramite il foglio di calcolo.
Da notare che l'utilizzo della Password numerica è alternativo all'uso di quella testuale, non si può fare 21 lanci e poi usare entrambe le password.
Se siete interessati a capire il funzionamento del foglio elettronico o a farvi i conti manualmente, date una occhiata alla sezione seguente intitolata "Elementi di conversione di basi".
Usiamo dei dadi non truccati, quindi è meglio se sono nuovi e li lanciamo come faremo in un casinò, supponiamo di fare una serie di lanci che numeriamo da 0 a 21 e registriamo il risultato, supponiamo sia:
sottraiamo da ogni Risultato l'unità e abbiamo:
Ora prendiamo una calcolatrice e convertiamo il numero qui sopra dalla base dei dadi (base 6) alla base decimale. Usando le potenze del 6, calcoliamo le potenze come 6 elevato al numero del lancio, prendiamo i lanci fino al N° 12:
612, 611, 610, ... , 62, 61, 60
2176782336, 362797056, 60466176, ... , 36, 6, 1
Andate avanti fino a quando la vostra calcolatrice vi permette di arrivare. Se non avete una calcolatrice scientifica moltiplicate il numero 1 per 6 tante volte quanto indicato dalla potenza: 1=1, 1·6=6, 6·6=36, 36·6=216, 216·6=1296, 1296·6=7776, ecc, ecc.
Ora moltiplicate la potenza per il Risultato del lancio corrispettivo ottenendo l'ultima riga, arrivate fino a dove potete, iniziando dal lancio N°0 e proseguite verso sinistra:
Adesso sommate tutti i numeri dell'ultima riga della tabella: Ris · 6N°
Fate attenzione a quando la vostra calcolatrice (sarebbe meglio usare un foglio elettronico oppure una calcolatrice a precisione infinita) smette di indicarvi il numero con tutte le cifre: fermatevi al numero prima. Partite dalla colonna N° 0 e proseguite verso sinistra.
Somma di Ris · 60, ... , Ris · 612: 10587974791
Bene, il numero ottenuto, in grassetto, è la conversione del lancio dei dadi in un numero in base 10. Possiamo usare il numero ottenuto (meno le prime cifre più significative) per la parte numerica della password, quindi per esempio se vogliamo 5 cifre, scegliamo le ultime 5 cifre ovvero:
74791
il resto lo gettiamo.
Adesso ripetiamo la procedura appena vista con un nuovo lancio dei dadi per ottenere una nuovo numero decimale. Supponiamo di avere ottenuto il numero:
Somma di Ris · 60, ... , Ris · 612: 21730562183
Vogliamo convertire questo numero in una serie di lettere dell'alfabeto italiano che ha 21 caratteri minuscoli: a,b, ..., u, v, z.
Dividiamo la Somma in grassetto per 21:
21730562183 : 21 = 1034788675 con il resto di 8
1034788675 : 21 = 49275651 con il resto di 4
49275651 : 21 = 2346459 con il resto di 12
2346459 : 21 = 111736 con il resto di 3
111736 : 21 = 5320 con il resto di 16
5320 : 21 = 253 con il resto di 7
253 : 21 = 12 con il resto di 1
12 : 21 = 0 con il resto di 12
Ora prendiamo tutti i resti e li mettiamo in una tabella in modo ordinato dal numero 0 al numero 7:
Convertiamo il Resto in una lettera dove: a=0, b=1, c=2, d=3, .. , u=18, v=19, z=20
Scartiamo le prime due lettere della tabella per esempio e otteniamo le prime 6 lettere della password:
hsdoei
Ripetiamo la procedura con un altro lancio dei dadi per ottenere le altre lettere casuali che ci servono per formare la password della lunghezza desiderata.
Problemi probabilistici nella conversione
Ci si chiederà come mai tagliare due o tre cifre dal numero casuale appena ottenuto. Supponiamo di fare due lanci di un dado a 6 facce, si otterranno due numeri che decrementati di 1 chiameremo: n0 e n1, se li convertiamo in decimale otteniamo il numero: n0 + n1 · 6. Ora il numero minimo che si può ottenere è 0 mentre il massimo numero decimale ottenibile è 35. Si può facilmente dimostrare che se i dadi non sono truccati ogni evento tra 0 e 35 ha la stessa probabilità che è pari a 1/36.
Se tiriamo il dado due volte otteniamo un numero decimale composto da due cifre che chiamiamo: x1 e x0 dove x1 è la cifra più significativa e variabile da 0 a 3, mentre la cifra meno significativa x0 è variabile tra 0 e 9.
Domanda: se prendiamo solo la cifra decimale meno significativa (x0) ci accorgiamo che se i dadi generano un numero decimale nell'intervallo 0-29 allora le cifre che stanno destra del numero hanno tutte la medesima probabilità, infatti abbiamo lo 0 presente nel numero: 0, 10, 20, la cifra 1 è in: 1, 11, 21, ... la cifra 9 è presente nei numeri: 9, 19, 29. Quindi sono equiprobabili.
Se lasciamo liberi i dadi di generare un qualsiasi numero equiprobabile da 0 a 35 con probabilità 1/36 abbiamo che la cifra meno significativa dello 0 si presenta in: 0, 10, 20, 30 con probabilità 4/36 (P[x0 = 0] = 4/36), analogamente per le cifre 1, 2, 3, 4, 5 aventi tutte probabilità 4/36. La cifra 6 è però presente solo in: 6, 16, 26 e ha quindi probabilità 3/46 (P[x0 = 6] = 3/36), analogamente per le cifre 7, 8, 9: queste ultime quattro cifre sono meno probabili e quindi l'attaccante potrebbe partire dai numeri 0-5 che sono più probabili e arrivare a scoprire prima la nostra password senza tentare tutte le combinazioni. Questo indebolisce la nostra password.
Supponiamo adesso di avere fatto molti lanci di dadi oltre ai primi due e supponiamo che la conversione in decimale sia un numero variabile tra 0 e 999+35, dove ritroviamo il 35 appena esaminato e quindi possiamo sfruttare l'analisi appena fatta. Ogni numero ha probabilità uguale e pari a 1/1035.
Ora la cifra meno significativa 0 è presente 10 volte tra 0-99, altre 10 tra 100-199, ... , altre 10 tra 900-999. In totale fanno 10·10 volte in cui è presente lo 0. Lo stesso avviene per le altre cifre: 1-9, sono tutte presenti 100 volte ciascuna.
Usiamo adesso l'analisi precedente sui numeri tra 0 e 35 con le cifre a destra 0-5 presenti 4 volte mentre quelle 6-9 sono presenti solo 3 volte. Uniamo i due risultati:
cifre meno significative 0-5 presenti ogni una: 100 volte + 4 volte = 104 volte
cifre meno significative 6-9 presenti ogni una: 100 volte + 3 volte = 103 volte
La probabilità per ogni evento del primo gruppo (0-5) è quindi: P[x0 = 0] = 104/1035
La probabilità per ogni evento del secondo gruppo (6-9) è quindi: P[x0 = 6] = 103/1035
La differenza di probabilità è in termini percentuali pari a:
P[x0 = 0] - P[x0 = 6]
----------------------- = 0.97% ≈ 1%
P[x0 = 6]
Se invece i lanci di dadi ci danno un numero decimale variabile tra 0 e 9999+35, la nostra cifra meno significativa (quindi scartando le 4 cifre più importanti e prendendo l'ultima) avrà una differenza di probabilità tra ogni evento dei due blocchi 0-5 e 6-9, pari a:
P[x0 = 0] - P[x0 = 6]
----------------------- = 0.1%
P[x0 = 6]
Quindi poco importante.
Riassumendo se scartiamo le prime 3 cifre decimali più significative della password numerica ottenuta dal lancio dei dadi, la 4a cifra ha una differenza percentuale della probabilità tra i vari eventi che è al massimo del 1%, la 5a è al massimo dello 0.1%, la sesta è al massimo dello 0.01% e così via.
Credit Image: cubo di Rubik it.wikipedia.org
Vediamo qualche esempio:
echo -n "password123"|sha256sumabbiamo applicato l'algoritmo di hash sha256 alla parola segreta:
ef92b778bafe771e89245b89ecbc08a44a4e166c06659911881f383d4473e94f
"password123"
e abbiamo ottenuto l'hash:
"ef92b778bafe771e89245b89ecbc08a44a4e166c06659911881f383d4473e94f"
Il problema del cracker è invertire l'hash ovvero lui ha a disposizione il numero esadecimale di 64 cifre qui sopra e deve trovare a che password corrisponde. L'unico modo di risolvere il problema è provare tutte le combinazioni di password, calcolare l'hash e poi vedere se l'hash calcolato corrisponde a quello che ha in mano. Se corrisponde allora ha trovato la parola segreta.
Poiché provare tutte le combinazioni è molto lungo si cercano delle scorciatoie e cioè si usa il fatto che le persone non sono dei computer e che tengono in mente solo parole segrete fatte in un certo modo. Per esempio la gente si ricorda una parola contenuta nei dizionari seguita da un numero oppure si ricorda uno schema di lettere che c'è nella tastiera, per esempio qwerty oppure qazwsxedc. La prima password, qwerty, non è altro che la prima riga delle lettere sulla tastiera, la seconda parola segreta, qazwsxedc, non è altro che le prime tre colonne delle lettere sulla tastiera.
I dizionari delle principali lingue contengono pochi termini, ogni uno circa 20 mila termini, quindi provando 100 mila password già si possono crakkare le parole segrete più facili. Infatti se supponiamo di prendere in considerazione 5 lingue, si ha che una password di una sola parola in una qualsiasi di queste 5 lingue è crakkabile in 5*20'000 tentativi. Aggiungendo alla fine della parola del dizionario tutti i numeri compresi tra 0 e 9999, si rende la ricerca un po' più difficile. In quest'ultimo caso i tentativi da fare ovvero gli hash da calcolare sono un po' di più ovvero 1 miliardo.
Nel caso si usi la forma della tastiera per inventarsi la parola segreta allora i tentativi da fare per il cracker non sono molti, probabilmente sotto i 10 mila considerando tutti i possibili schemi e anche con un numero finale di 4 cifre si sta sotto il miliardo.
Per il cracker il problema è quindi risolvibile con 2 miliardi di prove sia se usiamo una parola del dizionario sia se usiamo lo schema della tastiera. La domanda a questo punto è: ma quanto tempo impiega un computer per fare 2 miliardi di hash con l'algoritmo sha256? La risposta è: poco tempo.
Ci sono macchine che calcolano l'hash a miliardi in un secondo e comprando decine o migliaia di queste macchine (lo può fare lo Stato americano oppure la mafia o altre organizzazioni) si possono calcolare anche mille o più miliardi di hash al secondo. Quindi in un secondo la password che abbiamo visto sopra è scovabile.
Veniamo alla seconda domanda. C'è un limite a queste macchine che calcolano così tanti hash al secondo? La risposta è affermativa. Queste macchine che adesso si chiamano ASIC ma che in futuro si evolveranno in macchine più potenti, hanno un grosso limite ovvero consumano energia elettrica, ogni hash costa una certa energia spesa.
In Italia l'energia elettrica ha un prezzo all'utente finale di 20 centesimi di euro al chilowattora, a livello industriale costa meno della metà, quindi uno Stato può pagarla un po' meno ma ha comunque un costo ingente. All'estero la corrente si paga di meno ma comunque mai sotto il costo industriale di 6 centesimi di dollaro al chilowattora. L'energia costa dovunque.
Le migliori macchine di adesso, le ASIC, per calcolare mille miliardi di hash (1 Terahash) consumano 0.4 milionesimi di euro in corrente elettrica. Con gli ASIC la nostra password, quella vista sopra, ha un costo in termini energetici irrisorio, quindi non è una parola segreta "sicura".
Veniamo alla domanda che mi ha ispirato per scrivere questo testo:
Esiste una password che abbia un costo in corrente veramente alto?Certamente esiste, anzi si può determinare una password che abbia il costo energetico alto quanto si vuole. Detto questo la conseguenza è valutare cosa protegge la nostra password e che valore abbia l'informazione protetta dalla password. Se il valore fosse di 1 milione di euro allora il costo energetico per scovare la password deve essere pari ad almeno 1 milione di euro.
Facciamo qualche esempio. La password casuale VRnkgxqgTKoK è composta da sole lettere maiuscole e minuscole dell'alfabeto inglese e ha un numero di tentativi che il cracker deve fare per scovarla pari a 390877006486250192896. Considerando il costo di 0.4 milionesimi di euro per 1 miliardo di tentativi (Hash), si ha:
Il costo energetico è di 150 euro.
La password casuale iktpxmwritiw è composta da 12 lettere minuscole su un alfabeto inglese di 25 lettere e ha un numero di hash che il cracker deve calcolare per scovarla pari a 95428956661682176 con un costo elettrico relativo pari a 4 centesimi di euro.
Aggiungendo alla password qui sopra il numero finale casuale 7909 si aumenta il costo energetico e si arriva a 240 euro. La parola segreta complessiva è iktpxmwritiw7909.
In conclusione per proteggere una informazione che vale qualche centinaia di euro una password di 12 lettere minuscole casuali dell'alfabeto inglese seguita da un numero di 4 cifre casuali è sufficiente.
Generiamo tramite un computer o una app di un telefono una password completamente casuale (avendo abbastanza entropia) di 12 lettere prese però dall'alfabeto italiano di 21 caratteri, seguiti da un numero altrettanto casuale di 4 cifre. Valore: 30 euro. Il mio generatore mi ha dato:
zgrvuhstmdtg5218
Per memorizzare una tale parola segreta si può sfruttare una particolarità della mente umana e cioè che è facile memorizzare una storiella. Quindi creiamo una storiella che abbia come prima lettera delle parole le lettere zgrvuhstmdtg5218. Per quanto riguarda il numero va imparato a memoria.
La storiella va scelta con cura, per esempio:
Zoe Grugniva Ruspando Velocemente Un Hash. Stava Timidamente Mangiando Del Tartufo Grigio. 5218Questa storiella con il numero vale la bellezza di 30 euro ma una volta che è pubblica non vale più nulla quindi non rivelate a nessuno la vostra fiaba che protegge la password.
Per quanto riguarda creare la password generata in modo casuale ci sono moltissimi algoritmi che lo fanno: per Firefox ci sono addon che si installano con un click come pwgen.
Man mano che passano gli anni il costo energetico per hash diminuisce e si passa dagli attuali 0.4 milionesimi di euro per terahash a valori minori. È un processo lento in parte contrastato dal fatto che l'energia elettrica costa sempre di più. Tutte le organizzazioni e tutti i cracker sono sottoposti alla legge economica del costo dell'energia, nessuno escluso.
In particolare anche la NSA americana che si vocifera abbia mezzi potentissimi, non può scovare una password che abbia un valore pari all'intera ricchezza americana prodotta in un anno: il PIL USA. Lo stesso vale per la mafia ma entrambi hanno mezzi più efficaci per farci rivelare la parola segreta anche se non vogliamo rivelarla: Guantanamo per quanto riguarda gli americani e la lupara bianca per la mafia.
Per una password che non debba proteggere un grande valore si possono usare dei servizi on line oppure una app scaricata sul proprio cellulare. Un servizio è ad esempio quello di Proton Password-generator che impostato su password di 22 caratteri (alfabeto inglese), minuscolo, senza simboli e numeri da la pwd:
wqzdkdbemcadrvunxauavm
togliendo i caratteri del solo alfabeto inglese (jkwxy) si ha:
qzddbemcadrvunauavm (19 caratteri)
che è utile per fissare la nostra password casuale nella parte delle lettere dell'alfabeto italiano. Per i numeri usiamo il servizio on line per generare casualmente un numero di 4 cifre, ottengo:
2p01yf3hcbrv8t4qhhfp4w
estraggo le sole cifre ed ho:
2013844 (7 cifre)
A questo punto posso costruire la mia password completamente casuale prendendo i primi enne caratteri di «qzddbemcadrvunauavm» e le prime emme cifre di «2013844», ottenendo la password di n+m caratteri.
Elementi di calcolo combinatorio
Nei commenti un lettore mi ha chiesto come si calcolano tutti i tentativi da fare per scoprire una pwd (password). La risposta completa si trova nei libri di matematica ma qui diamo degli spunti.
Supponiamo di avere un alfabeto α di simboli di questo tipo:
α ={a, b, c}
e di avere una parola composta da due soli simboli. Quante parole differenti si possono formare? Il problema si può facilmente risolvere costruendo una matrice bidimensionale ovvero di dimensione 2 pari al numero di simboli della nostra parola (2):
| a |
b |
c |
|
| a |
aa |
ab |
ac |
| b |
ba |
bb |
bc |
| c |
ca | cb | cc |
mettendo nella casella prima la lettera corrispondente della riga e poi la lettera della colonna, formiamo per ogni casella una parola di due caratteri. Così abbiamo costruito tutte le combinazioni di una parola di due lettere con un alfabeto di 3 simboli. È facile rispondere quante sono le possibili combinazioni: sono 3×3 ovvero il numero di simboli di α elevato alla potenza 2 perché 2 è la lunghezza della parola: 32.
È facile immaginare che per trovare tutte le combinazioni di una parola di tre simboli del tipo «cab» è necessario passare dalla matrice bidimensionale a quella tridimensionale: un cubo di Rubik per intenderci. Con l'immaginazione pensiamo alla matrice qui sopra con l'aggiunta di tre simboli che escono dallo schermo verso di noi: a, b, c. Si formeranno 3×3×3 caselline cubiche, ogni una delle quali possiamo riempirla con la parola di tre simboli fatta prendendo prima la casella delle righe, poi quella delle colonne e poi quella che esce dallo schermo. L'immagine del cubo che segue può aiutare:

Tutte le possibili combinazione di una parola di tipo «cab» sono quindi 33 come le caselle del cubo qui sopra raffigurato. Analogamente per una parola di lunghezza 4 le combinazioni sono 34. Ecc, ecc. Se α ={a, b, c, d, e, f, g, h, i, l, m, n, o, p, q, r, s, t, u, v, z} una parola del tipo «qaz» ha 213 combinazioni perché corrisponde a un cubo di lato 21. Se la parola è di 12 lettere allora tutte le possibili combinazioni sono:
2112
Gli altri concetti sono una variante di questi concetti appena esposti come giustapporre due password: «zgrvuhstmdtg» + «5218» = «zgrvuhstmdtg5218» da un numero di combinazioni che è il prodotto del numero di combinazioni degli elementi.
Aggiornamento 27 gen 2024: Il sito Hash rate Index riporta dati sempre aggiornati relativi alle macchine per minare bitcoin, quel che ci interessa qui è quanto consumano le migliori macchine ASIC per fare Hash. Nella data di questo aggiornamento siamo arrivati a circa 26 joule per TH (Tera Hash).
Domanda: Quanto costa fare 1 mille miliardi di tentativi ovvero 1 THash?
Partiamo dalle basi e calcoliamo quanto è l'energia di 1 joule in termini di kWh:
1 kWh = 1000W×1h = 1000W×3600s = 3.6×106 j
1 j = 0.278×10-6 kWh
visto il costo dell'elettricità che di solito viene preso a livello industriale pari a:
0.06 €/kWh
si ha che l'energia consumata da queste macchine ASIC per minare 1 TH è pari a:
26 j = 26×0.278×10-6 kWh = 7.22×10-6 kWh
con un costo economico pari a:
Costo di 26 j = 7.22×10-6 kWh × 0.06 €/kWh = 0.433×10-6 €
con questa cifra si realizzano 1 TH ovvero:
1×1012 Hash
quindi il costo per Hash è pari a:
Costo di 1 Hash = Costo di 26 j / 1×1012 = 0.433×10-6 € / 1×1012 = 0.433×10-18 €
Kensan.it 1 € = Costo di 2.31×1018 Hash
All'incirca occorre realizzare una password che abbia un numero di combinazioni pari a 1018 per farla costare 1 € in prezzo dell'energia.
Visto che con 11 lettere minuscole e 4 numeri decimali completamente casuali si raggiunge il numero di combinazioni pari a:
Numero combinazioni password «abcdefghilm1234» = 2111 × 104 = 3.5×1018
si ha che questa lunghezza di password casuale ha un prezzo di 1 €. Occorre quindi aggiungere agli 11 caratteri minuscoli tante lettere quanto grande è il prezzo che vogliamo raggiungere. Ecco una tabellina:
| Lunghezza aggiuntiva |
Lunghezza totale |
Prezzo |
|---|---|---|
| 0 |
11 | 1 € |
| 1 |
12 | 21 € |
| 2 |
13 | 441 € |
| 3 |
14 | 9.2 k€ |
| 4 |
15 | 0.2 M€ |
| 5 |
16 | 4.1 M€ |
| 6 |
17 | 86 M€ |
| 7 |
18 | 1.8 G€ |
Cui aggiungere il numero da 4 cifre. Quindi già con una password di 16 caratteri e 4 cifre decimali ha un prezzo in energia pari al milione di euro, quindi sufficiente per molti usi.
Aggiornamento 30 mag 2024: Una notizia letta sul giornale on line HWupgrade ha attirato la mia attenzione su un caso di una persona molto attenta alla questione sicurezza informatica e che ha salvato una password di 20 caratteri generata da un generatore di password di nome RoboForm, in un file di testo crittografato con il programma TrueCrypt. Il file testuale crittografato era protetto da una password che la persona in questione non ha dimenticato ma sfortunatamente non ha eseguito alcun backup del file di testo.
Quella lunga parola di 20 caratteri era la porta d'ingresso per accedere a un portafoglio bitcoin (bitcoin wallet). Nel 2013, anno della creazione della parola segreta di 20 caratteri, il bitcoin valeva molto poco e il protagonista dell'articolo ne possedeva 43.6 per un totale di circa 4'000 € di allora. Forse per questo che il back up non era importante ma sfortuna volle che il file di testo crittografato da TrueCrypt andasse corrotto irrimediabilmente e con esso anche il suo contenuto, ovvero la lunga password.
Adesso che ogni bitcoin vale oltre 60 mila euro (63 mila in questo momento), il protagonista ha cercato ogni mezzo per accedere al bitcoin wallet contenente 43.6 BTC peer un valore di milioni di euro. Una coppia di Hacker si è incaricata del salvataggio (dietro compenso) e dato che il file di testo corrotto non esiste più, hanno puntato la loro attenzione sul generatore di password RoboForm, cercando di vedere se ci sono delle falle.
Infatti provare tutte le combinazioni di una parola di 20 caratteri che usi come simboli oltre che le 25 lettere dell'alfabeto inglese, altri 25 del maiuscolo, più i numeri e più i simboli, non è una operazione che si può eseguire prima della fine dell'universo e comunque non in tempi umani.
Hanno però visto che RoboForm non genera password casuali e che impostando la data dell'orologio del PC, le password generate erano limitate a un piccolo insieme. Hanno fatto delle ipotesi sulla data dal 1 marzo all'1 giugno 2013 e sui caratteri, ipotizzando che non contenesse simboli sempre per via di difetti di RoboForm che in alcuni/diversi casi non generava simboli speciali. Questo li ha portati a provare tutte le combinazioni di un numero limitato di password e a trovare la parola chiave di 20 caratteri che ha sbloccato il portafoglio bitcoin contenente 43.6 bitcoin.
Sicuramente la morale di questa storia è quella di fare il backup dei file importanti, soprattutto quando contengono password. Per quanto riguarda l'argomento di questo articolo ovvero la sicurezza di una password, il suggerimento è quello di non usare il tool come RoboForm o quelli da me indicati all'inizio del testo per creare parole segrete di una certa importanza.
Un metodo sicuro per generare lettere e numeri casuali è quella manuale e antico dei dadi, vediamo come.
Per facilitare il compito potete scaricare il foglio elettronico seguente e inserire i lanci ripetuti di un dado a 6 facce nella colonna "C" incorniciata di rosso con 21 lanci. Otterrete la Password numerica e quella testuale automaticamente ma di lunghezza limitata. Scartate i primi due o tre caratteri e le prime due o tre cifre in quanto non sono equiprobabili per via della conversione. Facendo altre serie di 21 lanci potete allungare la vostra password di quanto volete giustapponendo le password ottenute tramite il foglio di calcolo.
Da notare che l'utilizzo della Password numerica è alternativo all'uso di quella testuale, non si può fare 21 lanci e poi usare entrambe le password.
Se siete interessati a capire il funzionamento del foglio elettronico o a farvi i conti manualmente, date una occhiata alla sezione seguente intitolata "Elementi di conversione di basi".
Elementi di conversione di basi
Usiamo dei dadi non truccati, quindi è meglio se sono nuovi e li lanciamo come faremo in un casinò, supponiamo di fare una serie di lanci che numeriamo da 0 a 21 e registriamo il risultato, supponiamo sia:
| N° del lancio | 21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 | 0 |
| Risultato | 4 |
1 |
5 |
6 |
2 |
5 |
6 |
2 |
4 |
5 |
6 |
2 |
1 |
4 |
5 |
6 |
1 |
2 |
4 |
5 |
6 |
2 |
sottraiamo da ogni Risultato l'unità e abbiamo:
| N° del lancio | 21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 | 0 |
| Risultato | 3 |
0 |
4 |
5 |
1 |
4 |
5 |
1 |
3 |
4 |
5 |
1 |
0 |
3 |
4 |
5 |
0 |
1 |
3 |
4 |
5 |
1 |
Ora prendiamo una calcolatrice e convertiamo il numero qui sopra dalla base dei dadi (base 6) alla base decimale. Usando le potenze del 6, calcoliamo le potenze come 6 elevato al numero del lancio, prendiamo i lanci fino al N° 12:
612, 611, 610, ... , 62, 61, 60
2176782336, 362797056, 60466176, ... , 36, 6, 1
| N° del lancio | 12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 | 0 |
| 6N° | 2176782336 | 362797056 | 60466176 | 10077696 |
1679616 |
279936 |
46656 |
7776 |
1296 |
216 |
36 |
6 |
1 |
Andate avanti fino a quando la vostra calcolatrice vi permette di arrivare. Se non avete una calcolatrice scientifica moltiplicate il numero 1 per 6 tante volte quanto indicato dalla potenza: 1=1, 1·6=6, 6·6=36, 36·6=216, 216·6=1296, 1296·6=7776, ecc, ecc.
Ora moltiplicate la potenza per il Risultato del lancio corrispettivo ottenendo l'ultima riga, arrivate fino a dove potete, iniziando dal lancio N°0 e proseguite verso sinistra:
| N° del lancio | 12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 | 0 |
| 6N° | 2176782336 | 362797056 | 60466176 | 10077696 |
1679616 |
279936 |
46656 |
7776 |
1296 |
216 |
36 |
6 |
1 |
| Risultato | 4 |
5 |
1 |
0 |
3 |
4 |
5 |
0 |
1 |
3 |
4 |
5 |
1 |
| Ris · 6N° | 8707129344 |
1813985280 |
60466176 | 0 |
5038848 |
1119744 |
233280 | 0 |
1296 |
648 |
144 | 30 |
1 |
Adesso sommate tutti i numeri dell'ultima riga della tabella: Ris · 6N°
Fate attenzione a quando la vostra calcolatrice (sarebbe meglio usare un foglio elettronico oppure una calcolatrice a precisione infinita) smette di indicarvi il numero con tutte le cifre: fermatevi al numero prima. Partite dalla colonna N° 0 e proseguite verso sinistra.
Somma di Ris · 60, ... , Ris · 612: 10587974791
Bene, il numero ottenuto, in grassetto, è la conversione del lancio dei dadi in un numero in base 10. Possiamo usare il numero ottenuto (meno le prime cifre più significative) per la parte numerica della password, quindi per esempio se vogliamo 5 cifre, scegliamo le ultime 5 cifre ovvero:
74791
il resto lo gettiamo.
Adesso ripetiamo la procedura appena vista con un nuovo lancio dei dadi per ottenere una nuovo numero decimale. Supponiamo di avere ottenuto il numero:
Somma di Ris · 60, ... , Ris · 612: 21730562183
Vogliamo convertire questo numero in una serie di lettere dell'alfabeto italiano che ha 21 caratteri minuscoli: a,b, ..., u, v, z.
Dividiamo la Somma in grassetto per 21:
21730562183 : 21 = 1034788675 con il resto di 8
1034788675 : 21 = 49275651 con il resto di 4
49275651 : 21 = 2346459 con il resto di 12
2346459 : 21 = 111736 con il resto di 3
111736 : 21 = 5320 con il resto di 16
5320 : 21 = 253 con il resto di 7
253 : 21 = 12 con il resto di 1
12 : 21 = 0 con il resto di 12
Ora prendiamo tutti i resti e li mettiamo in una tabella in modo ordinato dal numero 0 al numero 7:
| N° | 7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
| Resto | 12 |
1 |
7 |
16 |
3 |
12 |
4 |
8 |
Convertiamo il Resto in una lettera dove: a=0, b=1, c=2, d=3, .. , u=18, v=19, z=20
| N° | 7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
| Resto | 12 |
1 |
7 |
16 |
3 |
12 |
4 |
8 |
| Lettera | o |
b |
h |
s |
d |
o |
e |
i |
Scartiamo le prime due lettere della tabella per esempio e otteniamo le prime 6 lettere della password:
hsdoei
Ripetiamo la procedura con un altro lancio dei dadi per ottenere le altre lettere casuali che ci servono per formare la password della lunghezza desiderata.
Problemi probabilistici nella conversione
Ci si chiederà come mai tagliare due o tre cifre dal numero casuale appena ottenuto. Supponiamo di fare due lanci di un dado a 6 facce, si otterranno due numeri che decrementati di 1 chiameremo: n0 e n1, se li convertiamo in decimale otteniamo il numero: n0 + n1 · 6. Ora il numero minimo che si può ottenere è 0 mentre il massimo numero decimale ottenibile è 35. Si può facilmente dimostrare che se i dadi non sono truccati ogni evento tra 0 e 35 ha la stessa probabilità che è pari a 1/36.
Se tiriamo il dado due volte otteniamo un numero decimale composto da due cifre che chiamiamo: x1 e x0 dove x1 è la cifra più significativa e variabile da 0 a 3, mentre la cifra meno significativa x0 è variabile tra 0 e 9.
Domanda: se prendiamo solo la cifra decimale meno significativa (x0) ci accorgiamo che se i dadi generano un numero decimale nell'intervallo 0-29 allora le cifre che stanno destra del numero hanno tutte la medesima probabilità, infatti abbiamo lo 0 presente nel numero: 0, 10, 20, la cifra 1 è in: 1, 11, 21, ... la cifra 9 è presente nei numeri: 9, 19, 29. Quindi sono equiprobabili.
Se lasciamo liberi i dadi di generare un qualsiasi numero equiprobabile da 0 a 35 con probabilità 1/36 abbiamo che la cifra meno significativa dello 0 si presenta in: 0, 10, 20, 30 con probabilità 4/36 (P[x0 = 0] = 4/36), analogamente per le cifre 1, 2, 3, 4, 5 aventi tutte probabilità 4/36. La cifra 6 è però presente solo in: 6, 16, 26 e ha quindi probabilità 3/46 (P[x0 = 6] = 3/36), analogamente per le cifre 7, 8, 9: queste ultime quattro cifre sono meno probabili e quindi l'attaccante potrebbe partire dai numeri 0-5 che sono più probabili e arrivare a scoprire prima la nostra password senza tentare tutte le combinazioni. Questo indebolisce la nostra password.
Supponiamo adesso di avere fatto molti lanci di dadi oltre ai primi due e supponiamo che la conversione in decimale sia un numero variabile tra 0 e 999+35, dove ritroviamo il 35 appena esaminato e quindi possiamo sfruttare l'analisi appena fatta. Ogni numero ha probabilità uguale e pari a 1/1035.
Ora la cifra meno significativa 0 è presente 10 volte tra 0-99, altre 10 tra 100-199, ... , altre 10 tra 900-999. In totale fanno 10·10 volte in cui è presente lo 0. Lo stesso avviene per le altre cifre: 1-9, sono tutte presenti 100 volte ciascuna.
Usiamo adesso l'analisi precedente sui numeri tra 0 e 35 con le cifre a destra 0-5 presenti 4 volte mentre quelle 6-9 sono presenti solo 3 volte. Uniamo i due risultati:
cifre meno significative 0-5 presenti ogni una: 100 volte + 4 volte = 104 volte
cifre meno significative 6-9 presenti ogni una: 100 volte + 3 volte = 103 volte
La probabilità per ogni evento del primo gruppo (0-5) è quindi: P[x0 = 0] = 104/1035
La probabilità per ogni evento del secondo gruppo (6-9) è quindi: P[x0 = 6] = 103/1035
La differenza di probabilità è in termini percentuali pari a:
P[x0 = 0] - P[x0 = 6]
----------------------- = 0.97% ≈ 1%
P[x0 = 6]
Se invece i lanci di dadi ci danno un numero decimale variabile tra 0 e 9999+35, la nostra cifra meno significativa (quindi scartando le 4 cifre più importanti e prendendo l'ultima) avrà una differenza di probabilità tra ogni evento dei due blocchi 0-5 e 6-9, pari a:
P[x0 = 0] - P[x0 = 6]
----------------------- = 0.1%
P[x0 = 6]
Quindi poco importante.
Riassumendo se scartiamo le prime 3 cifre decimali più significative della password numerica ottenuta dal lancio dei dadi, la 4a cifra ha una differenza percentuale della probabilità tra i vari eventi che è al massimo del 1%, la 5a è al massimo dello 0.1%, la sesta è al massimo dello 0.01% e così via.
Credit Image: cubo di Rubik it.wikipedia.org













> una sequenza di caratteri.
Il calcolo è semplice. Se la password è casuale allora il numero di combinazioni coincide col numero di tentativi da fare per scoprire la password.
Il numero di combinazioni è un calcolo semplice. Nel caso dei numeri di 4 cifre il numero di combinazioni è pari al prodotto del numero di combinazioni della prima cifra (0-9 cioè 10 combinazioni) moltiplicato per quello della seconda (10) moltiplicato per quella della terza (10) e per quello della quarta (10): in totale fanno 10^4 combinazioni.
Analogamente per le lettere. Se l'alfabeto è quello italiano minuscolo allora ogni posto del carattere può assumere i valori dalla a alla z che sono 21. Una coppia di caratteri possono andare dalla aa alla zz: le combinazioni sono 21*21.
Per capire che le combinazioni sono 21*21 basta immaginare una matrice:
abc.z
a *
b
c
.
z
la matrice ha 21*21 caselle e ogni casella ha la combinazione dell'intestazione della riga con quella della colonna (riga a con colonna z fa la combinazione az)
Analogamente per tre caratteri le combinazioni sono 21*21*21 ovvero 21^3 in quanto in questo caso abbiamo a che fare con un cubo. E via dicendo.
Con 12 lettere le combinazioni sono 21^12 che aggiunte al numero di combinazioni date dai 4 numeri si ha:
21^12*10^4
Spero adesso sia chiaro.
Anonimo il 16 gennaio 2017 con il titolo: carino ma.