Stimatore del tempo di attesa per
finire un download
Parte II
(varianza di ß)
Parte II
(varianza di ß)
| ads kensan.it |
| Telefono
Azzurro 1.96.96 Linea gratuita per Bambini Offri il 5xMille a Telefono Azzurro: C.F. 920 126 903 73 Per informazioni chiama il numero verde 800.090.335 Telefono Azzurro si finanzia esclusivamente con contributi volontari www.azzurro.it |
EMERGENCY www.emergency.it 5xMille C.F. 971 471 101 55 |
Definiamo la v.a. ß basandoci sulle v.a. di Poisson, tempi di interarrivo, xi:
| N | |
|
| ------------ | = ß | (2.1) |
| ∑ Ni=1 xi | |
|
r(N)=sum(x(i))
ßN è quindi:
ßN=N/r(N)
La sua densità è pari a:
f(b)=N * (ß*N)^N/(N-1)! * 1/b^(N 1) * e(-ß*N/b)
Ora si evince la non banalità del problema in quanto E[ßN] non coincide con ß*N. Molto probabilmente la coincidenza si ha in probabilità per N->∞. Mi chiedo se ha validità assumere come migliore stima della densità degli arrivi al posto di ß*N la media E[ßN] con densità ß*N.
Dai calcoli fatti con octave, generando una serie di N=30 campioni poissoniani con densità 0.1, risulta:
ß*N=0.0997
E[ßN]=0.103
E[ßN^2]=0.0110
var normalizzata= 0.0195
Sembrerebbe un po' troppo alta, rappresenta un errore del 20%, sembra che ci sia una precisione su ß data dalla media dei campioni, pari a circa 2-5%.
Nel plot che segue si vedono con le crocette verdi le sucessive ß(i) con i variabile da 1 a 30, le due linee orizzontali sono invece ß*N più o meno la varianza normalizzata.
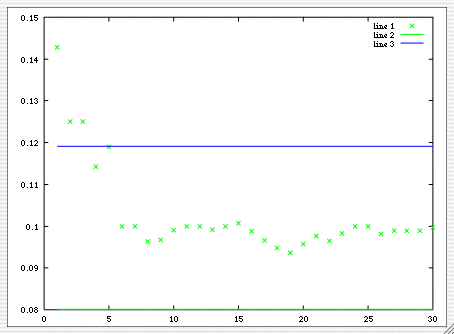
Figura 1
A questo punto approfondirò la teoria in particolare della Stima Bayesiana che pare la più recente e la più carina secondo Papoulis ma ho delle lacune sul concetto di funzione di variabile aleatoria condizionata da un'altra v.a..
Segue nella Appendice i calcoli Octave/MatLab utilizzati.
| Ciao Anonimo, commenta questo articolo! |
| NON ci sono ancora COMMENTI per questo articolo : |
|
|
| commenti abilitati per gli anonimi |
Commenti sperimentali
by kensan & Mp
by kensan & Mp
|
Sandro
kensan kensan.it Geek&Hacker site Owner, 1 ott 2003 |